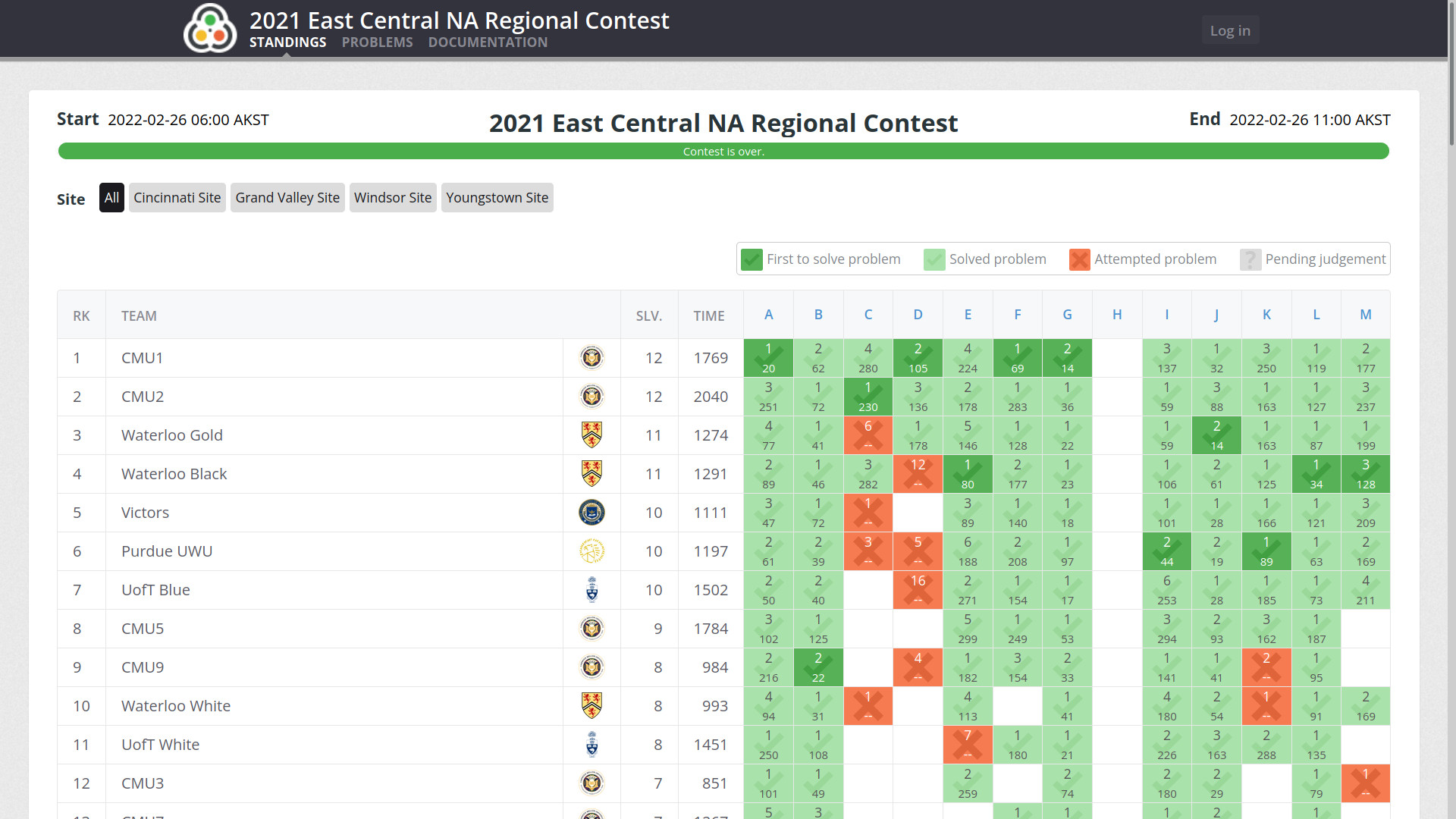
ACM-ICPC ECNA 2021 Solution
ACM-ICPC East Central North America Regional 2021 was held on Feb 27, 2022. Here is a link to the contest scoreboard, and I’m part of the team CMU9.
The contest was held on computer clusters on 5th floor of GHC, because the competition was remote this year. Here is a photo of the contest!

A. 1’s For All
Notice the unusual 15 second time limit. We can brute-force with a simple $O(n^2)$ DP and costs $5 \times 10^9$ time. And surprisingly, it passed the time limit!
B. Abridged Reading
We want to select arbitrary two leaf nodes and the costs is all its ancestors. So for any two leaf nodes, we can compute their LCA and then compute their cost.
C. Ball of Whacks
This problem looks too frustrating… I don’t like 3D objects.
D. Downsizing
If you plug in any curve to the equation of the corresponding line, you will find that each curve is a piece of another circle. Now you can calculate the circle area. You can add the area of sector in the circle (1), subtract the triangle from circle center to the endpoints (2), and add triangle from point O to the endpoints (3). Then you get the directional area and then sum up.
However, we got numerous Wrong Answer for this problem. There are two major issues. First, the line can intersect with the large circle. In this case, the generated circle has infinite radius and becomes a line, so you only need to calculate part (3). Second, when the circle sector is 180 degrees, you can’t determine whether it is $+180^\circ$ or $-180^\circ$. The two endpoints and the center of generated circle are on the same line. You will need to look at the sign of area (3) to determine the sign of (1).
E. Gambling Game
This is a probability DP problem. You can use $f[i][j]$ to represent the probability of winning when you have i square remaining on your paper while there are j ball announces left. Now you can easily determine the probability of current ball announce eliminating a square, because the number of balls remaining decreases one when the number of ball announces decrease one. Then you can use Python bigint to avoid writing bigint manually!
F. Growing Some Oobleck
This is a simuation problem. Every time when there exist circles to be merged, you simulate the merge operation. When there are no circles to be merged, you determine the next timestamp that a circle merge will happen, and fast forward to that time. Be careful of floating point precision problem!
G. Noonerized Spumbers
Brute-force all possible prefixes. Because all integers are smaller than $2^{31}$, the length of integers are at most 10. So it will work.
H. Numble
(I don’t know how to solve this)
I. Pinned Files
List the pinned elements and unpinned elements separately. First, in the optimal strategy, for any element, you operate on (pin/unpin) it at most twice. If you pin/unpin/pin element i, the result is equivalent to pin i at the timestamp of your last pin. If you pin/unpin/pin/unpin element j, the result is equivalent to pin/unpin j at the timestamp of last two operations (pin/unpin). Your previous operations to adjust the order become completely useless at the timestamp of your latest operation.
Now, for any element that begin in the pinned list and end in the unpinned list (or opposite), it can only be operated exactly once. For any element that begin and end in the same list, it can cost zero or two operations. We want to maximize the zero-operation element, so we can just greedily count how many elements do not need any operation.
J. Recycling
Use a monotone stack to compute the nearest element larger than itself to the left and to the right. Then loop over all elements to find the answer.
K. Stable Table
First, we can construct a directed graph, with “u => v” denoting if v is stable, then u is stable (equivalently, any square of node u is one square above any square of node v). We have a “top” set (containing at most 2 elements) and a “bottom” set, and we want the minimum number of paths from all top nodes toward any bottom node, and paths can be shared. We can start by a BFS with sources from all bottom nodes.
If there are one top nodes, we just want a simple shortest path, and this is computed in BFS. If there are two top nodes, denoted by root1 and root2, an existing solution is the sum of distance from bottom node to root1 and root2. But the two top nodes can also share path to reach any bottom node. Then the path should look like a fork: whenever two path intersect, they intersect until bottom node. Now we can do another two BFS from root1 and root2, then iterate over all nodes (to consider it as the potential path intersection), and its value is the sum of three BFS (starting from i to root1, root2 and bottom node).
L. Statues
We can iterate over all possible directions, and for any square, count if it exists on its corresponding diagonal. Then compute the minimum answer among all direction.
M. Tomb Hater
In this problem, because you can only move left/right/down, and you can visit one square only once, we know that we always visit a continuous segment on any line. Now we can maintain a Trie of the input strings, and make sure we are always staying on some node on the Trie. We can use DP with state $f[i][j][k]$ to represent we are currently on the i-th line, j-th column and Trie node k. Then we attempt to walk on the (i + 1)-th line and starting from column j. Notice that if we are on a Trie terminal node, we have the option of going back to root and continuing, so we have to maintain an array of all possible current Trie node.