CMU Computer Club is hosting Demosplash 2021! There are a lot of exciting machines!

Homecoming Week!

tyz is going to have a 18220 midterm next week so he is going to review some simple RLC circuits!

RC

Imagine there is a resistor and a capacitor connected in serial. Let $I_C$ be the current passing through the capacitor, $V_C$ be the voltage across the capacitor. Then the voltage across the resistor is $-V_C$. Assume the initial voltage across the capacitor is $V_0$.

Since $I_C = C{ {d V_C} \over {d t} }$, we have $R C{ {d V_C} \over {d t} } + V_C = 0$, and ${ {d V_C} \over {d t} } + {1 \over {RC} } V_C = 0$. Solving this equation we have $V_C = A e^{- {t \over {RC} } }$. Applying the initial value, we have $V_C = V_0 e^{- {t \over {RC} } }$. Let time constant $\tau = RC$, $V_C = V_0 e^{- {t \over \tau} }$

RC with voltage source

There is a resistor and a capacitor, and also a voltage source $V_0$ in serial. This time we assume initial voltage across the capacitor is 0V. As capacitor eventually become open circuit, we know the voltage across capacitor eventually becom $V_0$.

Since $I_C = C{ {d V_C} \over {d t} }$, we have $R C{ {d V_C} \over {d t} } + V_C = V_0$, or ${ {d V_C} \over {d t} } + { {V_C} \over {RC} } = { {V_0} \over {RC} }$. Solving this differential equation, we have $V_C = A e^{- {t \over {RC} } } + V0$. Applying initial value we have $V_C = A (1 - e^{- {t \over \tau} })$.

RL

Imagine there is a resisor and an inductor connected in serial. Let $I_L$ be the current passing through the inductor (and also the resistor), $V_L$ be the voltage across the inductor. Assume initial current passing the inductor is $I_0$.

Since $V_L = L { {d I_L} \over {dt} }$, we have $L { {d I_L} \over {dt} } + R I_L = 0$, or ${ {d I_L} \over {dt} } + {R \over L} I_L = 0$. Solving this we got $I_L = A e^{- {R \over L} t }$. Let $\tau = {L \over R}$ and applying initial value, we have $I_L = I_0 e^{- {t \over \tau} }$.

RL with voltage source

Now we have a voltage source $V_0$ in addition! As inductor eventually become short circuit, we know the current through the inductor eventually become $I_0$. Assume initial current through the inductor is 0A.

Since $V_L = L { {d I_L} \over {dt} }$, we have $L { {d I_L} \over {dt} } + R I_L = V_0$, ${ {d I_L} \over {dt} } + {R \over L} I_L = {V_0 \over L}$. So we have $I_L = {V_0 \over R} + A e^{- {t \over \tau} }$. Applying the initial value we have $I_L = {V_0 \over R} (1 - e^{- {t \over \tau} })$.

LC

Imagine there is a inductor and a capacitor in serial, and we want to know the voltage across the capacitor $V_C$. Then voltage across inductor is $-V_C$.

By $I = C{ {d V_C} \over {dt} }$ and $-V_C = L { {dI} \over {dt} }$, we have $-V_C = LC { {d^2 V_C} \over {dt^2} }$, or ${ {d^2 V_C} \over {dt^2} } + {V_C \over {LC} } = 0$. Let $\omega_0 = \sqrt{1 \over {LC} }$, we have $V_C = C_1 \cos (\omega_0 t) + C_2 \sin (\omega_0 t)$, and $V_C = R \sin (\omega_0 t + \phi)$.

RLC

Now suppose we have a resistor, a inductor and a capacitor in parallel! And we also want to know $V_C$.

Since $-V_C - IR = L { {dI} \over {dt} }$, we have ${ {d^2 V_C} \over {dt^2} } + {R \over L} { {d V_C} \over {dt} } + {V_C \over {LC} } = 0$. Let $\alpha = {R \over {2L} }$, solving $r^2 + 2\alpha r + (\omega_0)^2 = 0$. Now solution is (assume $\omega_0 > \alpha$), let $\mu = \sqrt{\omega_0 ^ 2 - \alpha ^ 2}$, $V_C = e ^ {-\alpha} (C_1 \cos (\mu t) + C_2 \sin (\mu t) )$, and $V_C = e ^ {-\alpha} R \sin (\mu t + \phi) $

Other circuits

For more complex circuits, we can always do nodal analysis! (QAQ)

1. Label nodes and their voltages
2. Write KCL formulas
3. For voltage source, create a new variable of the current flowing through it and add an equation about the voltage difference across it
4. For inductor, create a new variable of the current flowing through it and add an equation about the inductor voltage-current relation

MOSFET has the following operation regions:

• Cutoff region: When $V_{GS} < V_{TH}$. MOSFET acts like open circuit.

• Triode region: When $V_{GS} > V_{TH}$ and $V_{DS} < V_{GS} - V_{TH}$.
  In this region, the current flowing from drain to source is $I_{D} = {k \over 2} [ 2 (V_{GS} - V_{TH}) V_{DS} - V_{DS}^2 ]$. When $V_{DS}$ is very small, this is approximately $I_{D} = k (V_{GS} - V_{TH}) V_{DS}$ and the MOSFET can be regarded as a resistor of resistance $R_{ch} = k (V_{GS} - V_{TH})$.
  It’s common to use this region in digital circuit because it behaves like a digital switch whose resistance is either 0 or $R_{ch}$.

• Saturation region: When $V_{GS} > V_{TH}$ and $V_{DS} > V_{GS} - V_{TH}$.
  In this region, the current flowing from drain to source is $I_{D} = {k \over 2} ( V_{GS} - V_{TH} )^2$. The MOSFET can be regarded as a voltage-controlled current source.
  It’s common to use this region in analog circuit because it provides the largest gain from input $V_{GS}$.

The above are for NMOS. For PMOS, change the sign of $V_{GS}$, $V_{TH}$ and $V_{DS}$ and other things are similar.

Background

I like using Miniflux to read RSS feeds! Miniflux has a very nice web UI to read articles and manage feeds/categories. But sometimes I’m too lazy to open a browser to read news. So I decided to write a simple CLI client using Miniflux API.

Project Radiation

With Project Radiation, you can read news articles directly in your terminal! The program uses a command prompt to select between listing entry list, displaying article content, and switching to next/previous pages. And paging is supported both on entry list and article content. The default action (empty command) is to display the first available article and its consecutive pages, so that normally the only thing users needs to do is press Enter repeatedly. You can see the command prompt being “> “ in normal mode and “(id) >” in article paging mode (activated when an article has more than one page).

External Program

Lynx is used to convert article content formatted in HTML into text strings to display in terminal, and it is called using the exec package.

Conclusion

This is my first project using Go and programming in Go is fun! Returning error is more intuitive than the exception system in C++/Java and helps me write better error handling code, there are many useful packages built-in such as net/http and JSON encoding which is easy to use, calling external program and redirecting its stdin/stdout is easier than manually fork-exec-pipe-dup2 in C, and I implemented most features in Project Radiation faster than I expected.

Background

In recent days I was debugging some strange crashes of Project Railway. The railway process sometimes receives signal SIGSEGV when calling gst_player_new or gst_player_play. After switching to calling the mpg123 program by fork-exec as music playing backend, currently there are no crashes. Maybe I should write some documentation to explain the program.

RailwayMusic

RailwayMusic does the actual work by calling mpg123, using its remote control mode.

void init_music(): Constructor function; launch mpg123 and create read/write file pointers that sends to mpg123; launch music_wait thread.
void destroy_music(): Destructor function; cancel and wait for the thread; tells mpg123 to quit and wait for it.
void music_play(song_type*): Ask mpg123 to stop and load this song.
void music_volume(double): Pass volume to mpg123.
void music_pause_trigger(): Pass pause to mpg123.
bool music_is_playing(): Get the play state boolean.
void* music_wait(void*): Thread that continuously read output of mpg123.
int music_update(void*): Update function that run every 1 sec in the main thread to update progress bar and switch to next song if necessary.

RailwayPlaylist

RailwayPlaylist is a simple part to maintain current playlist. It contains the current track index in playlist_ptr.

void init_playlist(): Constructor function; init vars.
void destroy_playlist(): Destructor function; cleanup playlist_array if necessary; reset vars.
void generate_playlist(song_type*): Generate playlist array by cloning the current song_array.
void playlist_next(): Modify playlist_ptr; calls play_song to do actual music playing.
void playlist_prev(): Similar to playlist_next.
void playlist_play(song_type*): To play a new song that changes the playlist. First destroy and regenerate the playlist, and call play_song.
void playlist_set_shuffle(bool): Set shuffle status.
void playlist_set_repeat(bool): Set repeat status.

RailwayLib

RailwayLib manages the library of albums and songs, configuration file, and gets music tags to sort songs by track id.

void init_library(): Constructor function; get configuration values; init the gst_discoverer to get tags.
void destroy_library(): Destructor function; cleanup resources.
void generate_album_list(): To generate album_array; iterate over library directories and artist directories to generate a linked list of albums and convert to array (to find out number of albums and malloc accordingly).
void generate_song_list(const album_type*): To generate song_array; iterate over each (regular) song file in a given album directory; create linked list and song array.
void destroy_album_list(): Cleanup album array.
void destroy_song_list(): Cleanup song array.
void generate_album_button_image(GTask*, void*, album_type*, void*): Function for GTask thread to generate album cover picture; Get any song in the album; check if existing picture exist, and if not exist generate one using ffmpeg -n -i <song filename> <image filename>.

Railway

Railway controls all GUI elements and sets their handlers.

void music_position_update_cb(int, int): Update the song progress bar; called from update function in railwaymusic.
void music_pause_button_trigger_cb(GtkWidget*, void*): Update the icon of the play/pause trigger button; call railwaymusic to trigger pause.
void play_song(song_type*): Setting labels and images in the interface and pass to music_play; called from railwayplaylist.
void init_albums(): Create album button grid.
void destroy_albums(): Cleanup album button array.
void init_window() && void init_control(): Set signal handlers.
bool substring_test(const char*, const char*): Substring test (case insensitive).
bool search_judge(album_type*, const char*): Test if an album contains the given search term.

Background: I was using Rhythmbox to listen to music in GNOME desktop environment. Rhythmbox is an awesome and powerful music player. But several days ago, I think maybe browsing albums in the form of album cover picture grid will look better than browsing albums in album name list, so I start this project.

Project Railway is a Gtk+ music player. It consists of the following parts:

• railway: GUI part. Controls all widgets. Also, calls the ffmpeg program to generate album cover picture for each album asynchronously with GTask, to not block GUI with time-consuming operation.
• railwaylibrary: Reads music library and generates arrays of song and album information. And uses GStreamer GstDiscoverer to retrieve song metadata, or “tags”, to sort music in track order.
• railwaymusic: The actual music player part. Calls GStreamer GstPlayer to do all the work.
• railwayplaylist: Manages the playlist by cloning a copy of song array.

The resulting music player looks like:

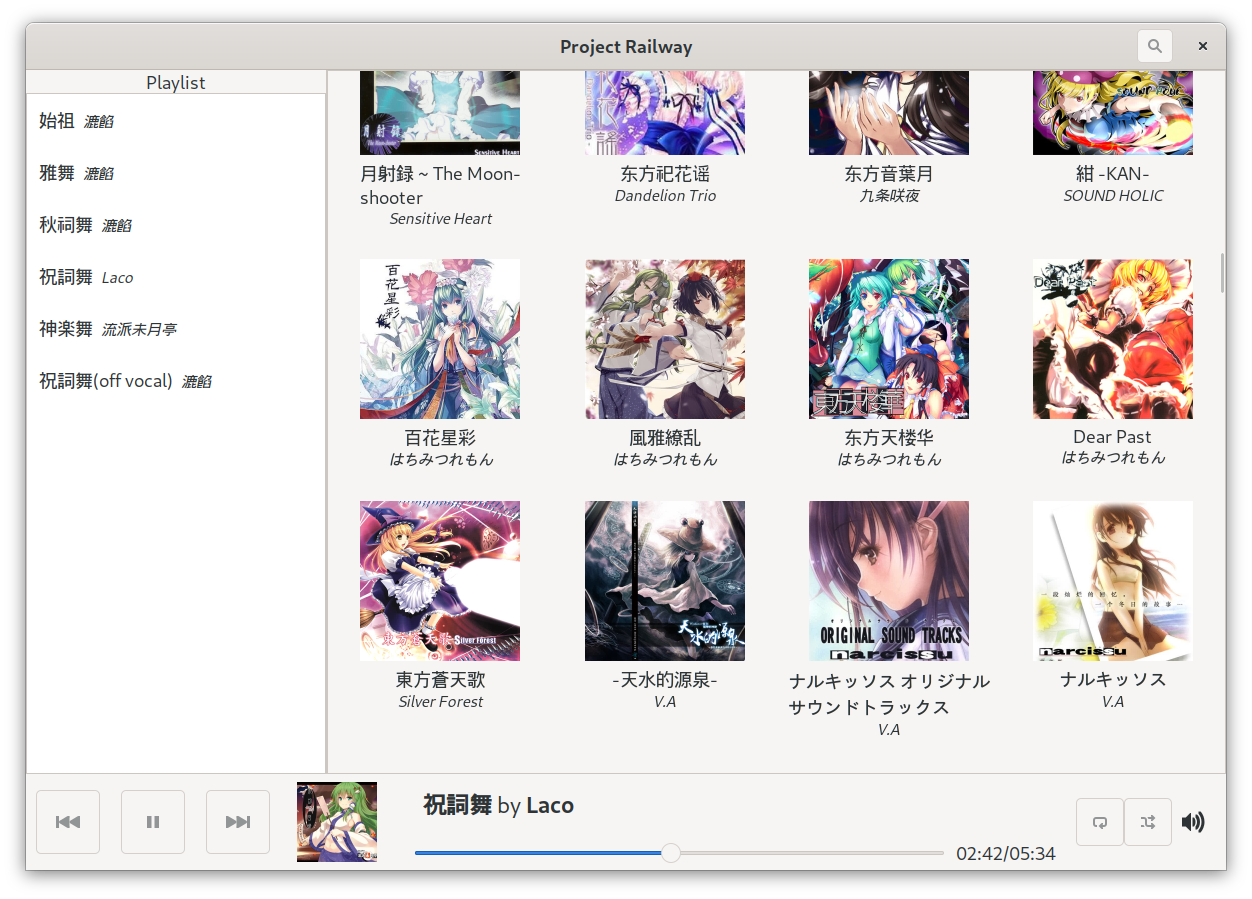
UPD: Support searching by album name or artist name now!

AMD YES!

Linux installs without any problem. The only issue is battery drain when poweroff (which is strange), and downgrading BIOS to version 1.29 solves this.

Project Ran is a javascript project. I’m learning js this summer because my previous web projects (like Project HTIC) rely on jumping to other pages to respond to any user action, which makes user experience not responsive.

Javascript has many interesting features. It is not typed (you can assign a variable with a string then an integer, like in Python). Functions can be defined directly into a variable and that variable can be called. Function can be used to create objects using the new operator. And JSON is native here.

Project Ran aims to implement a STG game similar to Touhou Project in javascript. In Touhou Eiyashou ~ Imperishable Night (東方永夜抄 ~ Imperishable Night), Yakumo Ran (八雲藍, blue) is the shikigami of Yakumo Yukari (八雲紫, purple). Ran is used as project name here because Ran is relatively like a computer.

I think the basic features of a STG game have been implemented, including entrance/game interfaces, bullet drawing and shooting, judge of player and enemy damage, high/low speed change, life/bomb counting, so at least it is runnable. But many things should be improved, including better art, game story, enemy characters, and better animations, like player start or bombing effect in 東方永夜抄. The animations look primitive now. It takes me many time and code to draw simple animation like circle animations at speedchange event.

The basic object for drawing things is shape. Then a bullet_array helps manage an array of shapes (bullets) shoot by player and enemy. A player or enemy has-a shape to represent themselves and a bullet_array to represent the bullets they shoot. A arena_game maintains currently active enemies, invoke player and enemy to draw and judge bullet damage. A game either has-a arena_game or a arena_text (which displays text on screen) depending on the story.

Spring 2021 马上就要结束了呢。

这个学期学到了很多有趣的内容！数学学了R2/R3上的微分（用partial derivative），积分（用Fubini Theorem和换元解决），以及scalar/vector surface integral。写作学了很多有用的知识（例如MLA格式，abstract, acknowledgement, Thesis-driven/IMRAD, novelty moves, 以及其他有趣的技巧）。计算机学了DFA, TM, Cook/Karp reduction, 随机/近似算法，还有对很多高级内容的入门。所以这个学期还是相当亦可赛艇的（笑）

暑假准备玩一下Go！